The next data type on the list is the Python set. The Python set can, such as the tuple (Python Course #9: Tuples) and the list (Python Course #8: Lists), store multiple values, however, a Python set does not have an order which is in accordance with the mathematical definition of a set. Two other key characteristics of Python sets are that they can’t store duplicates, and they are a mutable data type, so it is possible to add and remove values.
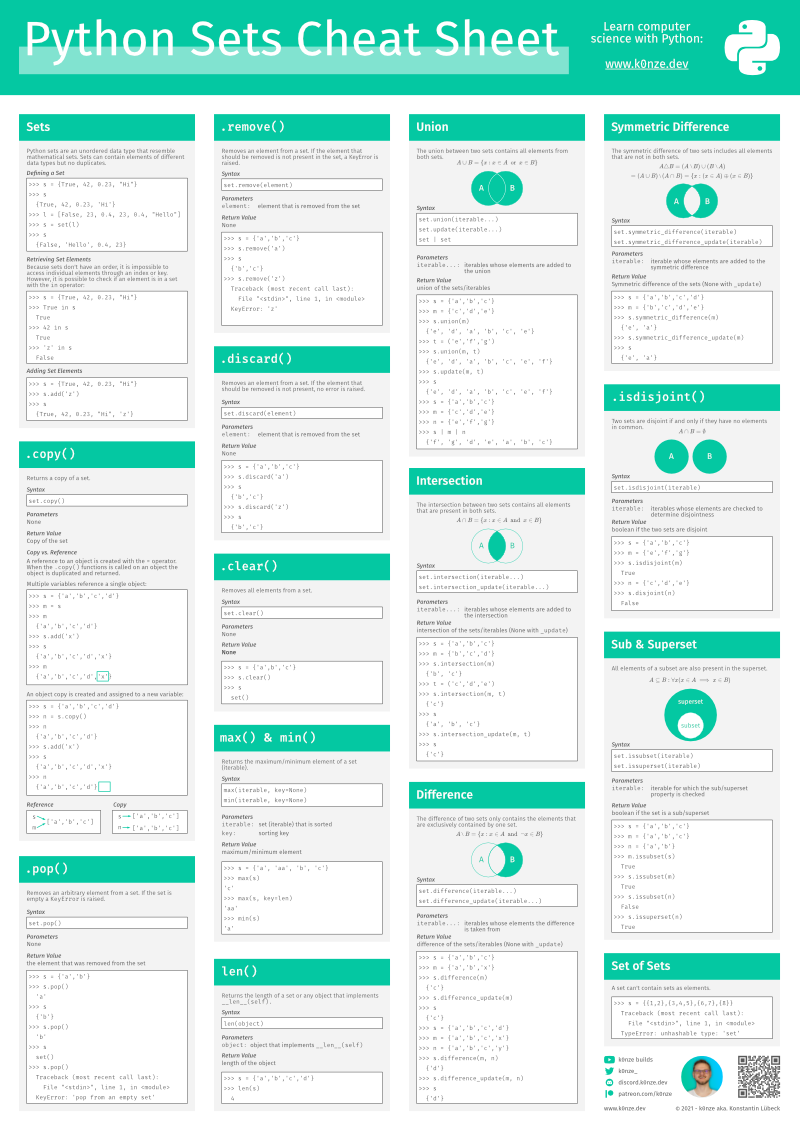
Free Python Sets Cheat Sheet
Pick up your free Python sets cheat sheet from my Gumroad shop:
Declaring a Python Set
Declaring a Python set works almost in the same way as declaring a tuple or a list where all elements are separated by a comma the elements themselves are enclosed by braces { }:
1
2
3
>>> s = {True, 42, 0.23, "Hi"}
>>> s
{0.23, True, 42, 'Hi'}
Accessing Python Set Elements
Becauce sets don’t have an order you are not able to access individual set elements. You can however check if an element is included in a set with the in operator:
1
2
3
4
5
>>> s = {'a', 'b', 'c', 'd'}
>>> 'a' in s
True
>>> 'z' in s
False
Adding new Elements to a Python Set
To add a single element to a set use the .add() function:
1
2
3
4
>>> s = {'a', 'b', 'c', 'd'}
>>> s.add('z')
>>> s
{'d', 'c', 'a', 'b', 'z'}
You can also add multiple elements to set coming from a list,tuple, or another set using the .update() function:
1
2
3
4
5
6
7
8
9
10
11
12
13
>>> s = {'a','b','c','d'}
>>> l = ['e', 'f', 'g']
>>> s.update(l)
>>> s
{'d', 'e', 'c', 'a', 'g', 'b', 'f'}
>>> t = ('h', 'i', 'j')
>>> s.update(t)
>>> s
{'i', 'd', 'e', 'c', 'h', 'a', 'j', 'g', 'b', 'f'}
>>> m = {'k','l','m'}
>>> s.update(m)
>>> s
{'k', 'i', 'd', 'e', 'c', 'h', 'm', 'a', 'j', 'g', 'b', 'l', 'f'}
When you try to add an element to a set that is already in the list nothing will be added because sets can’t contain duplicates:
1
2
3
4
5
6
7
>>> s = {'a','b','c','d'}
>>> s.add('a')
>>> s
{'b', 'd', 'a', 'c'}
>>> s.update(['c','x'])
>>> s
{'d', 'c', 'a', 'b', 'x'}
Removing Elements from a Python Set
There are actually two ways of removing an element from a set. The first one is .remove():
1
2
3
4
>>> s = {'a','b','c','d'}
>>> s.remove('a')
>>> s
{'b', 'd', 'c'}
However, if you want to remove an element that is not in a set you will get a KeyError:
1
2
3
4
5
>>> s = {'a','b','c','d'}
>>> s.remove('z')
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
KeyError: 'z'
This is where the second function for removing elements from a set comes into play. The .discard() function removes an element from a set in the same way the .remove() function does it with the key difference that when an element should be removed that is no containted in a set no error will be raised:
1
2
3
4
5
6
7
>>> s = {'a','b','c','d'}
>>> s.discard('a')
>>> s
{'b', 'd', 'c'}
>>> s.discard('z')
>>> s
{'b', 'd', 'c'}
Removing an arbitrary element from a Python set the .pop() function is used. .pop() removes a random element from a set and returns it:
1
2
3
>>> s = {'a','b','c','d'}
>>> s.pop()
'b'
To remove all elements from a set use the .clear() function which will turn your set into an empty set:
1
2
3
4
>>> s = {'a','b','c','d'}
>>> s.clear()
>>> s
set()
Python Set Functions
Next to the .add(), .update(), .remove(), etc. functions there are several other functions for Python sets that allow you to join sets and check their properties them in a very elegant way.
set()
The set() function turns every iterable such as tuples and lists into a set:
1
2
3
4
5
6
>>> l = ['a','b','c']
>>> set(l)
{'b', 'a', 'c'}
>>> t = (1,2,3)
>>> set(t)
{1, 2, 3}
The set() function can be very useful when you want to check any of the set properties on lists or tuples.
max() and min()
To find the maximum and minimum element of a set use max() and min(). When not passing any parameters to max() and min() they will return the maximum/minimum element of the alphanumeric order, however, you can set a key such as key=len to find the maximum/minimum element according to that key:
1
2
3
4
5
6
7
>>> s = {'a', 'aa', 'b', 'c'}
>>> max(sl)
'c'
>>> max(s, key=len)
'aa'
>>> min(s)
'a'
.union()
In the mathematical set theory a union of two sets creates a new set that contains all elements from both sets:
\[A \cup B = \{x: x \in A \hspace{0.5em}\text{or}\hspace{0.5em} x\in B\}\]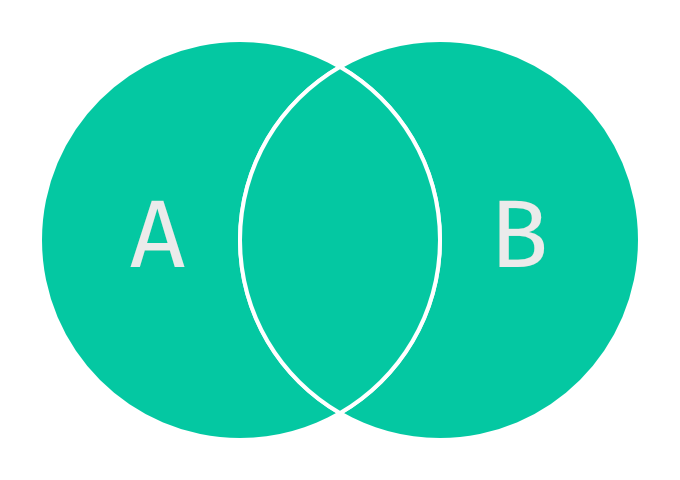
In Python you can also create a unions of sets:
1
2
3
4
>>> s = {'a','b'}
>>> m = {'b','c'}
>>> s.union(m)
{'b', 'a', 'c'}
You can not only join two sets in a union you can join as many as you want:
1
2
3
4
5
>>> s = {'a','b'}
>>> m = {'b','c'}
>>> n = {'x','z'}
>>> s.union(s,m,n)
{'a', 'z', 'b', 'c', 'x'}
The .update() function is a union with the slight difference that it does not return the union of the sets it updates the set on which .update() was called on with the union.
There is also a dedicated operator to unite sets which is the | pipe or bit-wise or:
1
2
3
4
>>> s = {'a','b'}
>>> m = {'b','c'}
>>> s | m
{'b', 'a', 'c'}
.intersection() and .intersection_update()
The inverse operation of the set union is the set intersection. An intersection of two sets only includes the elements that are in each set:
\[A \cap B = \{x: x \in A \hspace{0.5em}\text{and}\hspace{0.5em} x\in B\}\]
In Python the .intersection() function is used to intersect sets with each other:
1
2
3
4
5
>>> s = {'a','b','c'}
>>> m = {'b','c','d'}
>>> n = {'c','d','e'}
>>> s.intersection(m, n)
{'c'}
Python also provides the .intersection_update() function that allows you to store the intersection result in the set .intersection_update() was called on:
1
2
3
4
5
6
>>> s = {'a','b','c'}
>>> m = {'b','c','d'}
>>> n = {'c','d','e'}
>>> s.intersection_update(m, n)
>>> s
{'c'}
.difference() and .difference_update()
The difference of sets also called relative complement of two sets is a set that only contains elements that are not present in the other set:
\[A\setminus B = \{x: x\in A\hspace{0.5em}\text{and}\hspace{0.5em} \neg x\in B\}\]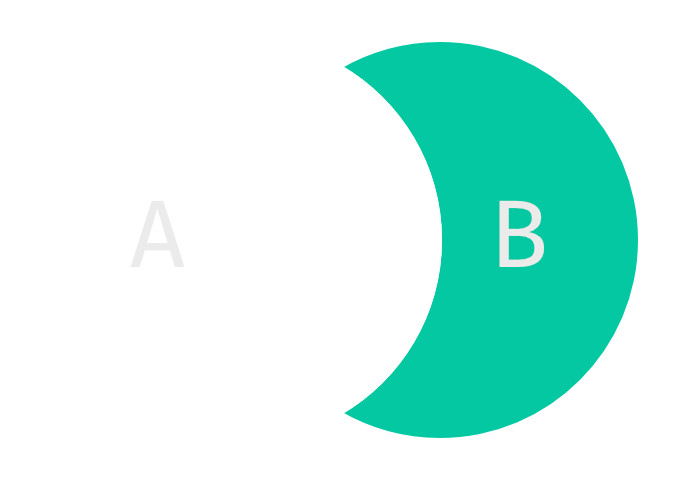
The Python set function for the set difference is .difference():
1
2
3
4
>>> s = {'a','b','c'}
>>> m = {'a','b','x'}
>>> s.difference(m)
{'c'}
Instead of returning the difference you can also update the set with .difference_update():
1
2
3
4
5
>>> s = {'a','b','c'}
>>> m = {'a','b','x'}
>>> s.difference_update(m)
>>> s
{'c'}
Both .difference() and .symmetric_difference() also support multiple sets as a arguments:
1
2
3
4
5
6
7
8
>>> s = {'a','b','c','d'}
>>> m = {'a','b','c','x'}
>>> n = {'a','b','c','y'}
>>> s.difference(m, n)
{'d'}
>>> s.difference_update(m, n)
>>> s
{'d'}
.symmetric_difference() and .symmetric_difference_update()
Closely related to the difference is the symmetric difference of sets. The symmetric difference of two sets includes all elements that are not in both sets. It can be expressed as the union of two differences where the sets change position, or as the difference of the union and the intersection:
\[A \triangle B = (A \setminus B) \cup (B \setminus A) = (A \cup B) \setminus (A \cap B) = \{x : (x \in A) \oplus (x \in B)\}\]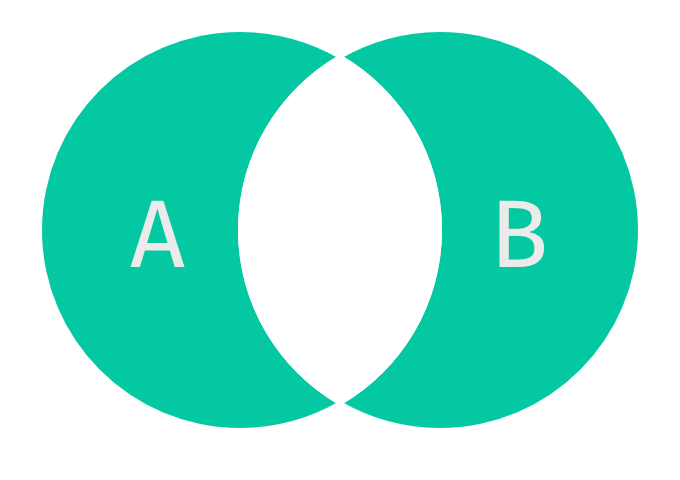
To get the symmetric difference in Python use the .symmetric_difference() and .symmetric_difference_update() functions, however, those functions only take one single set as a parameter:
1
2
3
4
5
6
7
>>> s = {'a','b','c','d'}
>>> m = {'b','c','d','e'}
>>> s.symmetric_difference(m)
{'e', 'a'}
>>> s.symmetric_difference_update(m)
>>> s
{'e', 'a'}
.isdisjoint()
It is often important to know if one set only contains elements not included in another set. When two sets contain elements that are not included in the other set, those sets are disjoint, or you could say the intersection of those twos sets is empty:
The Python function .isdisjoint() check the disjoint property for two given sets and returns the result as a bool:
1
2
3
4
5
6
7
>>> s = {'a','b','c'}
>>> m = {'d','e','f'}
>>> s.isdisjoint(m)
True
>>> n = {'b','c','d'}
>>> s.isdisjoint(n)
False
.issubset() and .issuperset()
The two last important set properties are if a set is completely included in another set. When all elements of a set are included in another set, this set is a subset while the other set is the superset.
\[A\subseteq B: \forall x \left(x \in A \implies x \in B\right)\]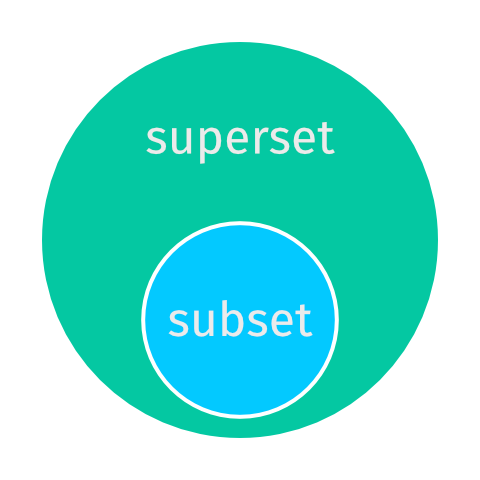
.issubset() and .issuperset() are the functions to check those properties and return a bool with the result:
1
2
3
4
5
6
7
8
9
10
11
>>> s = {'a','b','c'}
>>> m = {'a','b','c'}
>>> n = {'a','b'}
>>> m.issubset(s)
True
>>> s.issubset(m)
True
>>> s.issubset(n)
False
>>> s.issuperset(n)
True
len()
To get the length of a set use len():
1
2
3
>>> s = {'a','b','c'}
>>> len(s)
3
.copy()
As Python sets are an mutable data type they provide the .copy() function such as lists:
1
2
3
4
5
6
7
8
9
10
11
>>> s = {'a','b','c'}
>>> m = s
>>> n = s.copy()
>>> m.pop()
'b'
>>> s
{'a', 'c'}
>>> m
{'a', 'c'}
>>> n
{'b', 'a', 'c'}
The .copy() function concludes this article on Python sets. Make sure to get the free Python Sets Cheat Sheet in my Gumroad shop. If you have any questions about this article, feel free to join our Discord community to ask them over there.