With the knowledge of Python functions and algorithms, we are ready to write our first sorting algorithm and also take a closer look at how fast it runs.
What is a Sorting Algorithm
A sorting algorithm’s purpose is to reorder a list of elements based on a comparison criterion. This criterion is usually a less than operator < applied to the values of two numbers. However, you can use any comparison criterion that describes an order on the input data. For example, the a in strings could also be compared using a < comparison criterion. In this article, we are going to use integer numbers with < as a comparison criterion.
Insertion Sort Explained
When thinking about sorting numbers, the easiest way that comes to mind is to start at the second element and check if it is less than the first. If that is the case, the second element will be moved to the front, and the previous first element is moved one position to the back. The sub-list of the first and second elements is sorted, and the remainder of the list remains unsorted. Next, we pick the third element, and if you have to place it in front, in the middle, or the back of the sub-list consisting of the first and the second element. When we have found the correct spot, all elements greater than the selected third are moved one position to the back. Now the sub-list of the first three elements is sorted. And you might have already guessed it this is repeated until no elements are left in the unsorted part of the list. The following figure depicts a concrete example of how this sorting algorithm works:
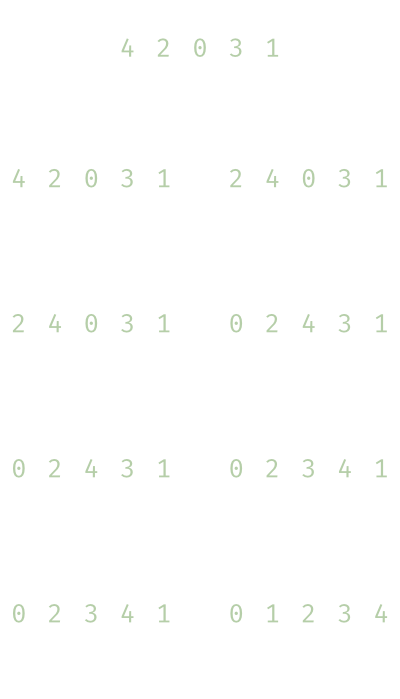
This kind of sorting algorithm is called insertion sort because every new element is inserted at the correct position of the sorted sub-list at the front. Insertion sort is a so-called in-place sorting algorithm which means that the sorting doesn’t happen in a second list; it takes place in the original list that is to be sorted.
Insertion Sort in Python
After looking at how the insertion sort algorithm works, we want to implement it in Python. As a first step, we are going to write a new function that checks if a list is sorted such that we have a quick way to verify that the sorting algorithm implementation is correct:
1
2
3
4
5
def is_sorted(l):
for i in range(len(l)-1):
if l[i] > l[i+1]:
return False
return True
The function is_sorted returns False if two consecutive elements of the input list l violate the <= comparison criterion. If all elements in the list l conform to the comparison criterion, the l is sorted, and True is returned. When implementing this, make sure that range(...) only goes to the second last element of l as in each iteration, two elements are accessed at position i and i+1. When range(...) would go to the last element of the l the last iteration would fail because l[i+1] tries to access an element outside of the l.
With a way to check if a list is sorted, we can move on to implement insertion sort in Python. When looking back at the figure, the algorithm picks an element in every step, which we will call key from now on, finds the correct position in the sorted sub-list in the front, and then moves all elements greater than key one position to the back. In the sub-list [0:1], the key is the element at position 0 and does not have to be moved; therefore, we are going to iterate over all element of the list starting from position 1 and pick those elements as key. Then we reverse iterate over the sorted sub-list to find the correct position for key and simultaneously move the elements greater than the key one element to the back. When we encounter an element in the sorted sub-list that is less than or equal to key we have found the correct position of key and can place it at this position:
1
2
3
4
5
6
7
8
9
10
11
12
13
def insertion_sort(l):
for j in range(1,len(l)):
key = l[j]
i = j - 1
while i >= 0 and l[i] > key:
l[i+1] = l[i]
i = i - 1
l[i+1] = key
if __name__ == "__main__":
l = [8,7,6,5,4,3,2,1,0]
insertion_sort(l)
print(is_sorted(l))
- in line 2 we iterate over the input list starting from position 1 as the sub list
[0:1]is already sorted. - in line 3 we pick
key, which is the first element not in the sorted sub-list. - in line 4 the index
iis initialized to the last position of the sorted sub-list. - in line 5
iis used to reverse iterate over the sortes sub list as long as elements in the sorted sub-list are greater thankey. - in line 6 the elements that are greater than
keyare moved one position to the back. - in line 7
iis decreased by one for the next iteration. - Lastly, in line 8
keyis placed at the correct position in sorted sub-list at ‘ i+1becausei` is decreased in every iteration of the while loop even though the correct position was found.
Now a list can be passed to insertion_sort(...), and the list will be sorted when it is finished.
Runtime of Insertion Sort
In computer science, it is always important to know how long an algorithm will take to process an input. One way to find out how long an algorithm takes is to measure the runtime; for example, you could use the Python timeit package to check the runtime of a piece of code. However, measuring the runtime will only tell you the runtime of the one input you have passed to the algorithm and is also of limited value because you only measured the runtime on your computer, which can hardly be transferred to a computer with a different hardware configuration. Therefore we need a more abstract way to firstly figure out the runtime of the algorithm depending on the input size and configuration and independent from the computer hardware itself.
The first step of getting such a runtime model of our insertion sort implementation is to assign each step or line of code an arbitrary but fixed runtime \(c_i\). In a second step, we count how often a line is executed depending on the input. Our insertion sort implementation consists of seven lines of code, not counting the function signature. All the lines indented under the for loop and the for loop head itself are executed \(n-1\) times while \(n\) denotes the length of the input list l (\(n =\) len(l)). the while loop head is executed \(n-1\) times multiplied with how often the while loop is executed. How often the while loop is executed depends on the input list l configuration. If l is already sorted the while loop never runs because l[i] > key is never True. If, however, the list l is sorted in reverse order, the while loop has to iterate j times which is the length of the sorted sub-list because key always has to be moved to the front of the sorted sub-list. We also remember that the while loop condition is always checked one time more than the code in the while loop is executed and is therefore executed j+1 times. To express that how often the while loop inside the for loop is executed we use a sum going from \(1\) to \(n-1\) over \(j\): \(\sum_{j=1}^{n-1} j\)
1
2
3
4
5
6
7
8
def insertion_sort(l):
for j in range(1,len(l)): # c_1 * (n-1)
key = l[j] # c_2 * (n-1
i = j - 1 # c_3 * (n-1)
while i >= 0 and l[i] > key: # c_4 * sum j to (n-1) (j+1)
l[i+1] = l[i] # c_5 * sum j to (n-1) j
i = i - 1 # c_6 * sum j to (n-1) j
l[i+1] = key # c_7 * (n-1)
Thinking in sums might not be super intuitive; therefore let us add some print statements to the insertion_sort(...) function and let it run with a list in reverse order visualize it:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def insertion_sort(l):
for j in range(1,len(l)):
key = l[j]
i = j - 1
print(f"j={j} ", end="")
while i >= 0 and l[i] > key:
print("*", end="")
l[i+1] = l[i]
i = i - 1
print()
l[i+1] = key
if __name__ == "__main__":
l = [4,3,2,1,0]
insertion_sort(l)
The output of the code above looks like this, where the asterisks * denote how often the while loop body was executed for a given j
1
2
3
4
j=1 *
j=2 **
j=3 ***
j=4 ****
When we sum up the asterisks, we get \(1+2+3+4\), and when we extend this to a list length of \(n\) we get the following sum:
\[\sum_{j=1}^{n-1} j\]Now we can add all annotations at the end of the lines togehter to get the platform independent run time for our insertion sort implementation depending on the input length:
\[T(n) = c_1 \cdot (n-1) + c_2 \cdot (n-1) + c_3 \cdot (n-1) + c_4 \cdot \sum_{j=1}^{n-1} (j+1) + c_5 \cdot \sum_{j=1}^{n-1} j + c_6 \cdot \sum_{j=1}^{n-1} j + c_7 \cdot (n-1)\]And When looking at that we first need to clean it up a little bit:
\[T(n) = (c_1+c_2+c_3+c_7) \cdot (n-1) + c_4 \cdot \sum_{j=1}^{n-1} (j+1) + (c_5+c_6) \cdot \sum_{j=1}^{n-1} j\]Now it looks a little bit cleaner. However, we still got the sums to convert into closed forms. But with the Gauß summation, this is not pretty easy. The Gauß summation states:
\[\sum_{i=1}^k = \frac{1}{2}k(k+1)\]We can replace \(i\) with \(j\) and \(k\) with \(n-1\) turn \(\sum_{j=1}^{n-1}\) into a closed form:
\[\sum_{j=1}^{n-1} j = \frac{1}{2}(n-1)(n-1+1) = \frac{1}{2}n(n-1)\]Now the sum has the same from as the first sum and we can replace it with the result from above:
\[\sum_{j=1}^{n-1} j = \frac{1}{2}(n-1)(n-1+1) = \frac{1}{2}n(n-1)\]For the second sum we first need to remove the \(+1\) from the sum body. With a little bit of thinking we can remove \(+1\) and add \(n-1\) to the whole sum because the sum adds \(n-1\) elements together and \(n-1\) times \(1\) is \(n-1\):
\[\sum_{j=1}^{n-1} (j+1) = \sum_{j=1}^{n-1} j + n-1 = \frac{1}{2}n(n-1) + n-1\]With the sum in closed from we replace the sums now separate the different powers of \(n\) from each other:
\[T(n) = (c_1+c_2+c_3+c_7) \cdot (n-1) + c_4 \cdot \left(\frac{1}{2}n(n-1)+n-1\right) + (c_5+c_6) \cdot \left(\frac{1}{2}n(n-1)\right)\]\[T(n) = \underbrace{(c_1+c_2+c_3+\frac{1}{2}c_4-\frac{1}{2}c_5-\frac{1}{2}c_6+c_7)}_a n+ \underbrace{\frac{1}{2}(c_4+c_5+c_6)}_b n^2 \underbrace{-c_1-c_2-c_3-c_4-c_7}_d\]And to get a clearer picture we substitue the all \(c_i\) with \(a\), \(b\), and \(c\) and get:
\[T(n) = a \cdot n + b\cdot n^2 - d\]This result shows us that our insertion sort algorithm has to execute \(n^2\) steps in the worst-case depending on the input length \(n\). We can also measure this effect by measuring the runtime for different inputs lengths and configurations:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import random
import timeit
import matplotlib.pyplot as plt
...
if __name__ == "__main__":
sizes = range(10, 1000, 10)
# best case
best_case_times = []
for size in sizes:
l = list(range(size))
start = timeit.default_timer()
insertion_sort(l)
stop = timeit.default_timer()
best_case_times.append(stop-start)
# average case
average_case_times = []
for size in sizes:
l = random.sample(range(0, size), size)
start = timeit.default_timer()
insertion_sort(l)
stop = timeit.default_timer()
average_case_times.append(stop-start)
# worst case
worst_case_times = []
for size in sizes:
l = list(range(size))
l.reverse()
start = timeit.default_timer()
insertion_sort(l)
stop = timeit.default_timer()
worst_case_times.append(stop-start)
fig, ax = plt.subplots()
ax.plot(sizes, best_case_times)
ax.plot(sizes, average_case_times)
ax.plot(sizes, worst_case_times)
ax.legend(["best-case", "average-case", "worst-case"])
plt.show()
The input list is already sorted in the best case, and the while loop body is never executed. In the average case, the input is randomized, and the number of times the loop body has to be executed is different for every for loop iteration. And lastly, in the worst case, the while loop body is executed $j$ times in every for loop iteration.

In the plot above, we can see the quadratic growth in runtime in the worst-case. The peaks in the graph are caused by the operating system, which we aren’t able to control at such a fine level.
There is an even more sophisticated method of determining and comparing runtimes of different algorithms with each other that is called the big-O method, which I’m going to cover in another article.